 Recognizing the patterns $\,x^n\,$ and $\,(-x)^n$
Recognizing the patterns $\,x^n\,$ and $\,(-x)^n$
You may want to explore these related concepts first: Equal or Opposites?
Examples
In the exercise, you will be filling in the blanks:
| The expression | $\,(-y)^{24}\,$ |
| is of the form | $\,(-x)^n\,$ |
| where $\,x\,$ is |
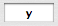
|
| and $\,n\,$ is |

|
Note that in the pattern $\,(-x)^n\,,$ the variable ‘$\,x\,$’ represents whatever comes after the minus sign, and the variable ‘$\,n\,$’ represents the exponent.
The expression
$\,(-3x)^{13}\,$ is of the form
$\,(-x)^n\,$
where
$\,x\,$ is
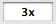 and
$\,n\,$ is
and
$\,n\,$ is
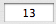 .
.
Try not to be confused by the appearance of the variable ‘$\,x\,$’ in two places! Again, we're matching something to the pattern $\,(-x)^n\,,$ where ‘$\,x\,$’ represents whatever comes after the minus sign. What comes after the minus sign in $\,(-3x)^{13}\,$? Answer: $\,3x\,$
The expression
$\,(-2x)^{7}\,$ is of the form
$\,x^n\,$
where
$\,x\,$ is
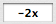 and
$\,n\,$ is
and
$\,n\,$ is
 .
.
Here, we're matching something to the pattern $\,x^n\,,$ so ‘$\,x\,$’ represents the entire base.