 Horizontal and Vertical Lines
Horizontal and Vertical Lines
Want some other practice with lines?
- Introduction to the Slope of a Line
- Practice with Slope
- Graphing Lines
- Finding Equations of Lines
- Point-Slope Form
Vertical and horizontal lines have equations that are simpler than all other lines!
Vertical lines have equations of the form: $$x = \text{some number}$$
Horizontal lines have equations of the form: $$y = \text{some number}$$
Why? Keep reading! Since they're commonly mixed up, two memory devices are offered, so you'll always get them right.
Vertical Lines
The points $\,(x,y)\,$ that satisfy the equation $\,x = 3\,$ (that is, $\,x + 0y = 3\,$) are all points of the form $\,(3,y)\,,$ where $\,y\,$ can be any real number. This is the vertical line that crosses the $\,x$-axis at $\,3\,.$
That is, in order to satisfy the equation $\,x =3\,,$ the $\,x$-value of a point must be $\,3\,.$ The $\,y$-value can be anything it wants to be. To get to any of these points from the origin, you move $\,3\,$ units to the right, and then up/down to your heart's content.
As a memory device, you might think of exaggerating the first stroke of the $\,x\,$ to make a vertical line.
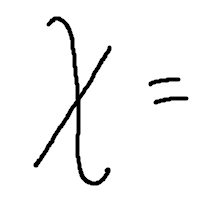 Memory Device for Vertical Lines
Memory Device for Vertical Lines
Horizontal Lines
The points $\,(x,y)\,$ that satisfy the equation $\,y = 3\,$ (that is, $\,0x + y = 3\,$) are all points of the form $\,(x,3)\,,$ where $\,x\,$ can be any real number. This is the horizontal line that crosses the $\,y$-axis at $\,3\,.$
That is, in order to satisfy the equation $\,y =3\,,$ the $\,y$-value of a point must be $\,3\,.$ The $\,x$-value can be anything it wants to be. To get to any of these points from the origin, you must move up $\,3\,$ units; you can move left/right to your heart's content.
As a memory device, you might think of exaggerating the $\,y\,$ to make a horizontal line. Draw a rising sun to remind you of the horizon!
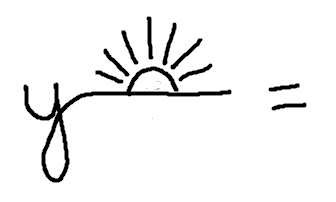 Memory Device for Horizontal Lines
Memory Device for Horizontal Lines
Equations of the form $\,x = k\,$ graph as vertical lines. The $\,y$-axis is a vertical line; its equation is $\,x = 0\,.$ All other vertical lines are parallel to the $\,y$-axis. All vertical lines are perpendicular to the $\,x$-axis. Vertical lines have no slope; i.e., the slope is not defined.
Equations of the form $\,y = k\,$ graph as horizontal lines. The $\,x$-axis is a horizontal line; its equation is $\,y=0\,.$ All other horizontal lines are parallel to the $\,x$-axis. Horizontal lines are perpendicular to the $\,y$-axis. Horizontal lines have slope $\,0\,$ (zero).