 Multiplying and Dividing Fractions with Variables
Multiplying and Dividing Fractions with Variables
To multiply and divide fractions with variables:
- Factor all numerators and denominators completely
- Use the rules for multiplying and dividing fractions:
(To multiply fractions, multiply ‘across’)
$$ \cssId{s7}{\frac{A}{B}\div\frac{C}{D}} \cssId{s8}{= \frac{A}{B}\cdot\frac{D}{C}} \cssId{s9}{= \frac{AD}{BC}} $$(To divide by a fraction, instead multiply by its reciprocal)
- Cancel any common factors; that is, get rid of any extra ‘factors of $\,1\,$’
- Leave your final answer in factored form
Example
Multiply, and write your answer in simplest form:
$$ \cssId{s16}{\frac{x^2-9}{5x^2+20x+15}} \cssId{s17}{\cdot} \cssId{s18}{\frac{x+1}{x+4}} $$|
$\displaystyle
\cssId{s20}{\frac{x^2-9}{5x^2+20x+15}}
\cssId{s21}{\cdot}
\cssId{s22}{\frac{x+1}{x+4}}
$ $\displaystyle \cssId{s23}{=} \cssId{s24}{\frac{(x-3)(x+3)}{5(x^2+4x+3)}} \cssId{s25}{\cdot} \cssId{s26}{\frac{x+1}{x+4}} $ |
factor: difference of squares (numerator), common factor (denominator) |
| $ \displaystyle \cssId{s30}{=} \cssId{s31}{\frac{(x-3)(x+3)}{5(x+3)(x+1)}} \cssId{s32}{\cdot} \cssId{s33}{\frac{x+1}{x+4}} $ | factor the trinomial in the denominator |
| $\displaystyle \cssId{s35}{=} \cssId{s36}{\frac{\hphantom{5}(x+1)(x+3)(x-3)}{5(x+1)(x+3)(x+4)}} $ | multiply, re-order |
| $\displaystyle \cssId{s38}{=} \cssId{s39}{\frac{(x-3)}{5(x+4)}} $ | cancel the two extra factors of $\,1\,$ |
It is interesting to compare the original expression (before simplification), and the simplified expression (after cancellation). Although they are equal for almost all values of $\,x\,,$ they do differ a bit, because of the cancellation:
[The next table is best viewed wide. On small screens, please use landscape mode.]
| Values of $\,x\,$ |
Original Expression: $$ \cssId{s47}{\frac{x^2-9}{5x^2+20x+15} \cdot \frac{x+1}{x+4}} $$In factored form: $$ \cssId{s49}{\frac{\hphantom{5}(x+1)(x+3)(x-3)}{5(x+1)(x+3)(x+4)}} $$ |
Simplified Expression: $$ \cssId{s51}{\frac{(x-3)}{5(x+4)}} $$ |
Comparison |
| $x = -4$ | not defined (division by zero) | not defined (division by zero) | behave the same: both are not defined |
| $x = -1$ | not defined (division by zero) | $$ \cssId{s60}{\frac{-1-3}{5(-1+4)} = -\frac{4}{15}} $$ | the presence of $\,\frac{x+1}{x+1}\,$ causes a puncture point at $\,x = -1\,$; see the first graph below |
| $x = -3$ | not defined (division by zero) | $$ \frac{-3-3}{5(-3+4)} = -\frac{6}{5} $$ | the presence of $\,\frac{x+3}{x+3}\,$ causes a puncture point at $\,x = -3\,$; see the first graph below |
| all other values of $\,x\,$ | both defined; values are equal | behave the same: values are equal | |
Graph of
$\displaystyle
\cssId{s72}{\frac{\hphantom{5}(x+1)(x+3)(x-3)}{5(x+1)(x+3)(x+4)}}
$
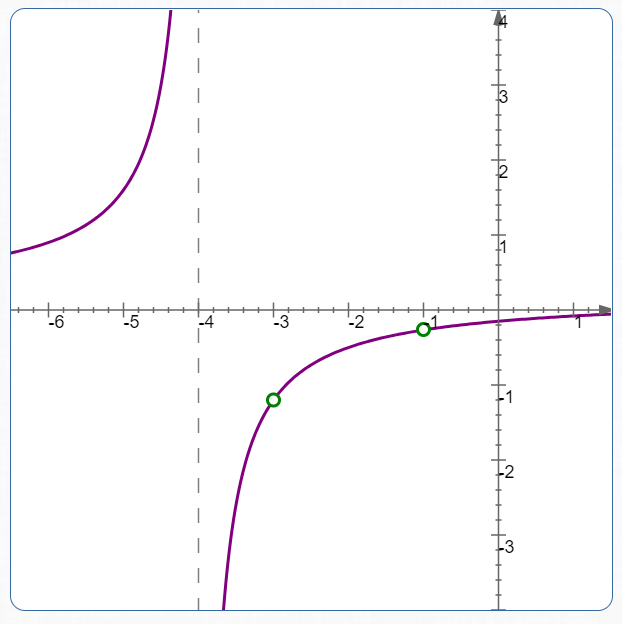
Graph of:
$\displaystyle
\cssId{s74}{\frac{(x-3)}{5(x+4)}}
$
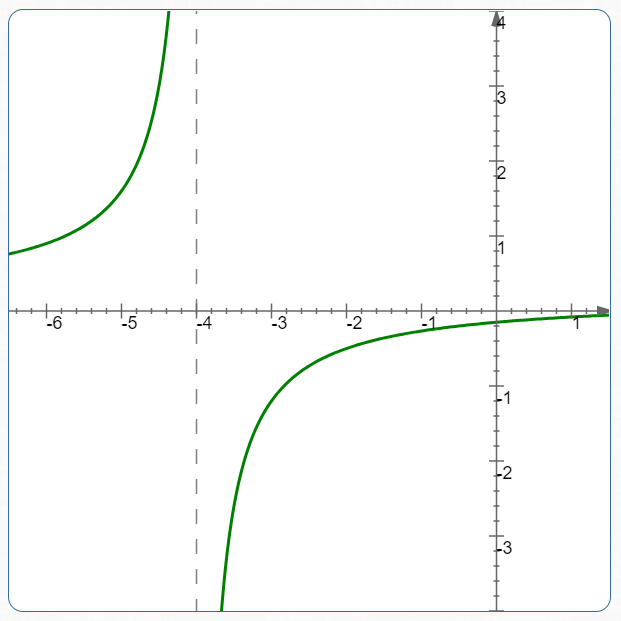
Concept Practice
For more advanced students, a graph is available. For example, the expression $\,\frac{x+1}{x+2}\cdot\frac{x+3}{x+1}\,$ is optionally accompanied by the graph of $\,y = \frac{x+1}{x+2}\cdot\frac{x+3}{x+1}\,.$ A puncture point occurs at $\,x = -1\,,$ due to the presence of $\,\frac{x+1}{x+1}\,.$ The graph of the simplified expression would not have this puncture point.
Horizontal/vertical asymptote(s) are shown in light grey. Note: A puncture point may occasionally occur outside the viewing window. Use the arrows in the lower-right graph corner to navigate left/up/down/right.
Click the ‘Show/Hide Graph’ button to toggle the graph.