 Probability Tree Diagrams
Probability Tree Diagrams
Want some preliminary probability information first?
A tree diagram represents the outcomes from a multi-step experiment.
A sample tree diagram is shown below. Repeatedly click the button to get many more (randomly-generated) samples!
Two-Step Probability Tree Diagrams
A multi-step experiment has more than one step. For example, here are some two-step experiments:
- Flip a coin and record Head or Tail (first step), then do it again (second step)
- Choose a ball from an urn and record its color, then do it again
- Flip a coin and record Head or Tail, then choose a ball from an urn and record its color
The branches emanating from any point on a tree diagram must have probabilities that sum to $\,1\,.$
In the sample tree diagram above (initial configuration), we have:
- $0.7 + 0.3 = 1$
- $0.2 + 0.7 + 0.1 = 1$
- $0.4 + 0.5 + 0.1 = 1$
To find the probability of any path, multiply the probabilities on the corresponding branches.
In the sample tree diagram above (initial configuration), there are six paths (going from top to bottom):
- $(0.7)(0.2) = 0.14$
- $(0.7)(0.7) = 0.49$
- $(0.7)(0.1) = 0.07$
- $(0.3)(0.4) = 0.12$
- $(0.3)(0.5) = 0.15$
- $(0.3)(0.1) = 0.03$
Notice that: $$\cssId{s31}{0.14 + 0.49 + 0.07 + 0.12 + 0.15 + 0.03 = 1}$$ Always do this check on your own probability tree diagrams!
Examples
Two Flips of a Fair Coin
Consider the two-step experiment ‘two flips of a fair coin’. Let H denote Head, and T denote Tail.
Note that the sample space for this experiment is: $$\cssId{s38}{S = \{\text{HH},\text{HT},\text{TH},\text{TT}\,\}}$$
The probability tree diagram is shown below.
Two Flips of a Fair Coin
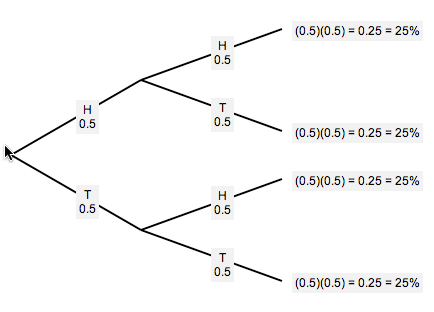
From the tree diagram, we can easily compute various probabilities:
$$ \begin{align} &\cssId{s41}{P(\text{both heads})}\cr &\quad \cssId{s42}{= P(\text{HH})} \cssId{s43}{= (0.5)(0.5)} \cssId{s44}{= 0.25}\cr\cr &\cssId{s45}{P(\text{both tails})}\cr &\quad \cssId{s46}{= P(\text{TT})} \cssId{s47}{= (0.5)(0.5)} \cssId{s48}{= 0.25}\cr\cr &\cssId{s49}{P(\text{no heads})}\cr &\quad \cssId{s50}{= P(\text{TT})} \cssId{s51}{= 0.25}\cr\cr &\cssId{s52}{P(\text{at least one head})}\cr &\quad \cssId{s53}{= P(\text{HH or HT or TH})}\cr &\quad \cssId{s54}{= P(\text{HH}) + P(\text{HT}) + P(\text{TH})}\cr &\quad \cssId{s55}{= 0.25 + 0.25 + 0.25 = 0.75}\cr\cr &\cssId{s56}{\text{alternative method:}}\cr &\cssId{s57}{P(\text{at least one head})}\cr &\quad \cssId{s58}{= P(\text{not TT})}\cr &\quad \cssId{s59}{= 1 - P(\text{TT})}\cr &\quad \cssId{s60}{= 1 - 0.25 = 0.75}\cr\cr &\cssId{s61}{P(\text{exactly one head})}\cr &\quad \cssId{s62}{= P(\text{HT or TH})}\cr &\quad \cssId{s63}{= P(\text{HT}) + P(\text{TH})}\cr &\quad \cssId{s64}{= 0.25 + 0.25 = 0.50} \end{align} $$Balls in an Urn, With Replacement
Suppose that an urn contains $\,2\,$ black balls, $\,1\,$ red ball, and $\,4\,$ green balls.
Two balls are chosen, with replacement, from the urn. That is: after the first ball is chosen and its color is recorded, it is returned to the urn. Assume that all balls are equally likely to be chosen.
Note that the sample space for this experiment is: $$\cssId{s72}{S = \{\text{BB},\text{BR},\text{BG},\text{RB},\text{RR},\text{RG},\text{GB},\text{GR},\text{GG}\}}$$
The probability tree diagram is shown below.
Balls in an Urn, With Replacement
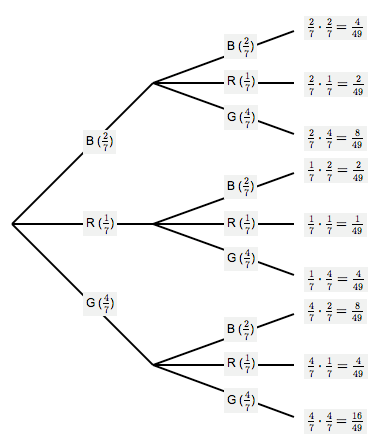
From the tree diagram, we can easily compute various probabilities:
$$ \begin{align} \cssId{s75}{P(\text{BB})} &\ \cssId{s76}{= \frac27\cdot\frac27} \cssId{s77}{= \frac4{49}}\cr\cr \cssId{s78}{P(\text{RR})} &\ \cssId{s79}{= \frac17\cdot\frac17} \cssId{s80}{= \frac1{49}}\cr\cr \cssId{s81}{P(\text{GG})} &\ \cssId{s82}{= \frac47\cdot\frac47} \cssId{s83}{= \frac{16}{49}}\cr\cr \cssId{s84}{P(\text{BB or RR})} &\ \cssId{s85}{= P(\text{BB}) + P(\text{RR})}\cr &\ \cssId{s86}{= \frac4{49} + \frac1{49}}\cr &\ \cssId{s87}{= \frac5{49}}\cr\cr \end{align} $$ $$ \begin{align} &\cssId{s88}{P(\text{at least one black ball is drawn})}\cr &\qquad \cssId{s89}{= P(\text{BB or BR or BG or RB or GB})}\cr &\qquad \cssId{s90}{= \frac4{49} + \frac2{49} + \frac8{49} + \frac2{49} + \frac8{49}}\cr &\qquad \cssId{s91}{= \frac{24}{49}}\cr\cr &\cssId{s92}{P(\text{at most one black ball is drawn})}\cr &\qquad \cssId{s93}{= P(\text{exactly one black ball or no black balls})}\cr &\qquad \cssId{s94}{= P(\text{all outcomes except BB})}\cr &\qquad \cssId{s95}{= 1 - \frac4{49}}\cr &\qquad \cssId{s96}{= \frac{45}{49}}\cr\cr &\cssId{s97}{P(\text{exactly one black ball is drawn})}\cr &\qquad \cssId{s98}{= P(\text{BR or BG or RB or GB})}\cr &\qquad \cssId{s99}{= \frac2{49} + \frac8{49} + \frac2{49} + \frac8{49}}\cr &\qquad \cssId{s100}{= \frac{20}{49}}\cr\cr &\cssId{s101}{P(\text{two different color balls})}\cr &\qquad \cssId{s102}{= P(\text{all outcomes except BB, RR, GG})}\cr &\qquad \cssId{s103}{= 1 - \frac4{49} - \frac1{49} - \frac{16}{49}}\cr &\qquad \cssId{s104}{= \frac{28}{49}} \end{align} $$Balls in an Urn, Without Replacement
Suppose that an urn contains $\,2\,$ black balls, $\,1\,$ red ball, and $\,4\,$ green balls.
Two balls are chosen, without replacement, from the urn. That is, the first ball is chosen and its color is recorded. It is not returned to the urn. Then, the second ball is chosen. Assume that all balls are equally likely to be chosen.
Note that the sample space for this experiment is: $$\cssId{s113}{S = \{\text{BB},\text{BR},\text{BG},\text{RB},\text{RG},\text{GB},\text{GR},\text{GG}\}}$$
There is no ‘RR’ in the sample space, since if a red ball is chosen on the first draw, then there are no red balls remaining in the urn.
The probability tree diagram is shown below.
Balls in an Urn, Without Replacement
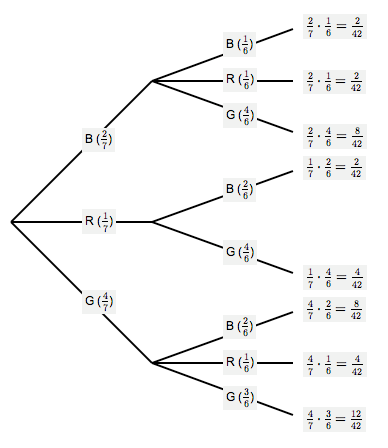
From the tree diagram, we can easily compute various probabilities:
$$ \begin{gather} \cssId{s119}{P(\text{BB})} \cssId{s120}{= \frac27 \cdot \frac16} \cssId{s121}{= \frac2{42}} \cssId{s122}{= \frac{1}{21}}\cr\cr \cssId{s123}{P(\text{RR}) = 0}\cr\cr \cssId{s124}{P(\text{GG})} \cssId{s125}{= \frac47 \cdot \frac36} \cssId{s126}{= \frac{12}{42}} \cssId{s127}{= \frac{2}{7}}\cr\cr \end{gather} $$ $$ \begin{align} &\cssId{s128}{P(\text{the same color is drawn twice})}\cr &\qquad \cssId{s129}{= P(\text{BB or GG})}\cr &\qquad \cssId{s130}{= \frac1{21} + \frac2{7} = \frac1{21} + \frac6{21}}\cr &\qquad \cssId{s131}{= \frac{7}{21} = \frac13}\cr\cr \end{align} $$ $$ \begin{gather} \cssId{s132}{P(\text{BR})} \cssId{s133}{= \frac27 \cdot \frac16} \cssId{s134}{= \frac2{42}} \cssId{s135}{= \frac{1}{21}}\cr\cr \cssId{s136}{P(\text{RB})} \cssId{s137}{= \frac17 \cdot \frac26} \cssId{s138}{= \frac2{42}} \cssId{s139}{= \frac{1}{21}}\cr\cr \end{gather} $$ $$ \begin{align} &\cssId{s140}{P(\text{a black ball and a red ball are drawn})}\cr &\qquad \cssId{s141}{= P(\text{BR or RB})}\cr &\qquad \cssId{s142}{= \frac1{21} + \frac1{21}}\cr &\qquad \cssId{s143}{= \frac{2}{21}} \end{align} $$Concept Practice
If a problem gives probabilities in decimal form, then give your answers in decimal form.
If a problem gives probabilities in fraction form, then give your answers as fractions in simplest form.