Arithmetic and Geometric Sequences
Arithmetic and Geometric Sequences
Need some practice with recursion and sequences first? Introduction to Recursion and Sequences
Note: When you talk about an arithmetic sequence, the word arithmetic (in this context) is pronounced air-ith-ME-tic; that is, the accent is on the third syllable.
Here, $\,d\,$ is called the common difference.
In an arithmetic sequence, each term is equal to the previous term, plus (or minus) a constant.
Example
The sequence $\,4\,,$ $\,7\,,$ $\,10\,,$ $\,13\,,$ $\,\ldots\,$ is an arithmetic sequence. The common difference is $\,3\,.$ To go from term to term, you keep adding $\,3\,.$
Connection Between Arithmetic Sequences and Linear Functions
Recall that linear functions graph as lines, and have a very special property: equal changes in the input give rise to equal changes in the output.
Arithmetic sequences have this same special property: equal changes in the input (e.g., moving from term to term) give rise to equal changes in the output (determined by the common difference). Thus, arithmetic sequences always graph as points along a line.
The graph of the sequence $\,4\,,$ $\,7\,,$ $\,10\,,$ $\,13\,,$ $\,\ldots\,$ is the set of points (‘dots’) shown below. When the input is $\,1\,$ (for the first term in the sequence), the output is $\,4\,.$ When the input is $\,2\,$ (for the second term in the sequence), the output is $\,7\,.$ When the input is $\,3\,$ (for the third term in the sequence), the output is $\,10\,,$ and so on.
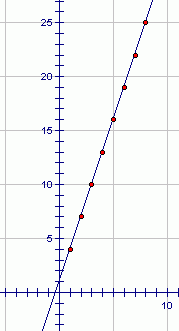
Example (arithmetic sequence)
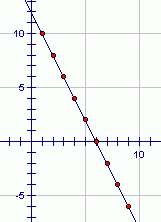
The sequence $\,10\,,$ $\,8\,,$ $\,6\,,$ $\,4\,,$ $\,\ldots\,$ is an arithmetic sequence. The common difference is $\,-2\,.$ To go from term to term, you keep adding $\,-2\,$ (i.e., subtracting $\,2\,$).
The graph of the sequence $\,10\,,$ $\,8\,,$ $\,6\,,$ $\,4\,,$ $\,\ldots\,$ is shown below:
A geometric sequence is a sequence of the form $\,u_n = r\cdot u_{n-1}\,.$
Here, $\,r\,$ is called the common ratio.
In a geometric sequence, each term is equal to the previous term, multiplied (or divided) by a constant.
Example (geometric sequence)
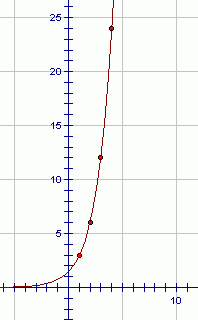
The sequence $\,3\,,$ $\,6\,,$ $\,12\,,$ $\,24\,,$ $\,\ldots\,$ is a geometric sequence. The common ratio is $\,2\,.$ To go from term to term, you keep multiplying by $\,2\,.$
Connection Between Geometric Sequences and Exponential Functions
There is a class of functions, called exponential functions, that have a very special property: equal changes in the input cause the output to be successively multiplied by a constant.
Geometric sequences have this same special property: equal changes in the input (e.g., moving from term to term) cause the output to be successively multiplied by a constant (determined by the common ratio). Thus, geometric sequences always graph as points along the graph of an exponential function.
The graph of the sequence $\,3\,,$ $\,6\,,$ $\,12\,,$ $\,24\,,$ $\,\ldots\,$ is shown below:
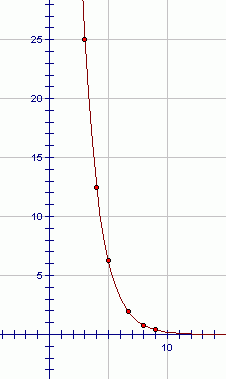
Example (geometric sequence)
The sequence $\,100\,,$ $\,50\,,$ $\,25\,,$ $\,12.5\,,$ $\,\ldots\,$ is a geometric sequence. The common ratio is $\,\frac{1}{2}\,.$ To go from term to term, you keep multiplying by $\,\frac{1}{2}\,$ (i.e., dividing by $\,2\,$).
The graph of the sequence $\,100\,,$ $\,50\,,$ $\,25\,,$ $\,12.5\,,$ $\,\ldots\,$ is shown below: